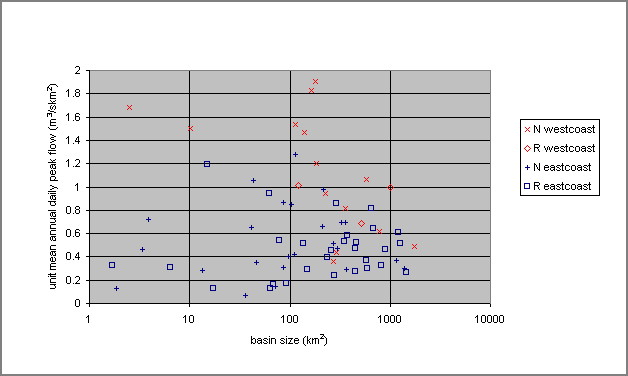
Figure 1: AREA VERSUS UNIT DAILY MEAN
TABLE OF CONTENTS
ABSTRACT
INTRODUCTION
OVERVIEW OF APPROACHES FOR ESTIMATING FLOWS FOR
DESING PURPOSES
FLOW
ESTIMATES BASED ON STREAM GEOMETRY
METHODS
BASED ON RAINFALL DATA
STATISTICAL
APPROACH
REGIONAL FLOOD
DATA
Mean Daily Peak
Flow
Coefficient of Variation
CONCLUSION
APPENDIX
ACKNOWLEDGEMENTS
REFERENCES
Published by the Canadian Water Resources
Association in the 1998 CWRA 51st Annual
Conference Proceedings, "Mountains to Sea: Human Interaction
with the Hydrologic Cycle." This article is posted with
permission from the Canadian Water Resources Association. [For
more information visit the CWRA web site.]
ESTIMATING PEAK FLOWS FROM FORESTED WATERSHEDS IN BRITISH COLUMBIA
By Lynne Tolland, Christian Zurbrugg, and S.O. Denis Russell
ABSTRACT
Information on peak flows with a specified return period is required for the design of forest road stream crossings. Traditionally, peak flows have been estimated by a variety of methods including the rational method and rainfall runoff models that assume that peak flows result from rainfall. In British Columbia, however, large floods frequently have a significant snowmelt component. This suggests that for much of the province, estimating flows on the basis of rainfall alone is not appropriate. A more realistic and robust approach is needed for these areas. A statistical approach is proposed. This involves estimating the mean annual peak flow for a particular site on the basis of local information and its coefficient of variation on the basis of regional information. Annual peak flows can be estimated from the stream geometry or by measuring the peak water levels upstream of existing culverts, which have entrance controls, as do most culverts in British Columbia. The approach is illustrated with data from Vancouver Island and a peak stage gauge, which has proven successful, is described.
In the province of British Columbia (BC), the Forest Practices Code specifies the 100 year instantaneous peak flow (Q100) for the design of bridges and culverts for stream crossings under forest roads. There are many hydrologic tools available for estimating design floods, but there is no generally agreed approach to choosing the most appropriate ones for use in BC; and, in any event, there is usually not enough data to allow reliable use of any of them (Tolland et al., 1998). With each designer tending to use a personally preferred approach, there can be a wide range in the estimates of the design flow for a particular project, if several designers are involved. Also, with user friendly computer programs becoming more readily accessible to practitioners, there is a danger that designers may not be aware of the limitations of the programs they are using. Thus, there seems to be a need for standardization of the approaches used for estimating design flows for forest road crossings, somewhat similar to the standardization of approaches to urban drainage that took place in the early 1970’s (Denver Regional Council of Governments, 1969).
OVERVIEW OF APPROACHES TO ESTIMATING FLOWS FOR DESIGN PURPOSES
Estimates of design flows in a particular stream have to be based on data. There is nothing in hydrology that would allow one to compute flows on the basis of theory alone, without local data. Since Q100 is required for design in BC, the database must have been collected over a sufficient period of years to provide a basis for extrapolation to 100 years. One can make an estimate of the average annual peak flow at the crossing site in question on the basis of local data on the stream geometry. It is, however, necessary to rely on either long-term rainfall data (in the case of floods that result almost entirely from rainfall) or on long-term flow data to include the time dimension. The Atmospheric Environment Service (AES) of Environment Canada measures and records rainfall intensities at widely spaced locations in Canada; and the Water Survey of Canada measures and records flows, including peak flows on streams throughout the country. However, most of the gauged streams are medium to large and the gauging stations are also widely spaced. Thus, except in the highly unlikely event of there being a flow gauge on the stream near the site of interest, one has to rely on regional data to estimate the multiplier needed convert the mean annual flow to Q100.
FLOW ESTIMATES BASED ON STREAM GEOMETRY
The Forest Practices Code of BC provides a simple way of sizing flow passages for streams under road crossings. This is based on the California Method and involves estimating the high water level in the stream, measuring the cross sectional area of the stream to that level, and then providing a culvert or bridge opening with three times that cross sectional area. This is a conservative approach, but it has the virtues of simplicity and being based on actual data at the site in question. The multiplier of three is an approximate upper limit of the ratio of Q100 to the mean annual peak flood, obtained from the gauged streams in the province. This method is used mainly for culverts of less than 2.0 metre diameter, above which size a professional engineer must complete the design.
A slightly more sophisticated approach involves first estimating the flow corresponding to the high water level, multiplying the flow by 3.0 to obtain Q100, and then designing the culvert or bridge to carry that flow. The flow in the stream can be estimated by Manning’s formula (Linsley et al., 1982; Maidment, 1992). However, with steep creeks where there is tumbling flow, one has to be careful as Manning’s formula overestimates the flow.
METHODS BASED ON RAINFALL DATA
One of the earliest and best known techniques for estimating peak flows is the rational method. It was developed mainly for estimating urban drainage flows for storm sewer design and it generally only produces reliable results in small watersheds where the input parameters can be properly quantified. The equation is:
Q = CiA (1)
where Q is the design flow in cfs; C is a coefficient that estimates the fraction of rainfall that runs off (the rest is assumed to sink into the ground and not appear in the stream until after the peak has passed); i is the average rainfall intensity during the time of concentration (in/hr); and A is the drainage area in acres. Practical difficulties arise in estimating "C" and "i". Generally, the rational method is believed to overestimate flow in rural, non-urban basins (Heimstra and Reich, 1969). Other estimation methods used in BC are the Burkli-Ziegler Equation and the Talbot Method, both essentially modifications of the rational formula (Watts, 1983). These methods use the runoff coefficient as a parameter, as well as basin response time or time of concentration (the time it takes the water to flow from the highest point in the watershed to the point of interest).
Another more sophisticated method of estimating flood flows on the basis of rainfall data is to use a rainfall-runoff model. These models require more types of information and more complex calculations, but computer versions are now available that require no more input data than the rational method. At present, they are used mainly with larger streams which have bridge crossings, rather than culverts. One such program is Hydrocad, which uses a rainfall-runoff model developed by the Soil Conservation Service (SCS) in the United States. It is necessary to provide this model with the time of concentration; a value of CN (curve number); the 24-hour 100 year rainfall and the rainfall distribution. The time of concentration (Tc) value can be estimated by the modified Snyder method (Linsley et al., 1982) using the following coefficients derived by Loukas (1996):
Tc = 0.60[L/2S0.5]0.38 (2)
where L is the length of the main stream in the basin in km; and S is the mean slope of the main stream in m/m. The CN value, which is similar to "C" in the rational method, describes the average permeability of the watershed. It can be estimated from tables in hydrology texts such as Chow et al. (1988) and checked against local data. The 24-hour rainfall data can be obtained from the nearest AES station; and the rainfall distribution can be specified as the SCS Type 1A distribution, which was developed by the SCS. It is given in hydrology texts such as Chow et al. (1988) and is "built in" to many computer programs such as Hydrocad. In his research, Loukas (1995) found the SCS Type 1A rainfall distribution to be slightly conservative, but otherwise quite suitable for the large frontal rainstorms that occur in winter on or near the coast of BC.
A problem with techniques that use rainfall is that rainfall measurements are often only taken at valley bottom locations, which may not be representative of rainfall over the watershed areas, which in BC, are typically steep with large elevation ranges and correspondingly steep rainfall gradients. An even more serious problem with rainfall based methods for computing design flows is that in almost all of BC, except in the extreme southwestern portion of the province, there is a significant element of snowmelt in most of the larger floods. Along the coast, there are many "rain-on-snow" floods in the fall and winter and often these are the largest floods of the year. In the interior, floods mainly result from snowmelt, although there can be a significant rainfall component to the flood peaks. For these situations, rainfall based flood estimating methods cannot produce reliable estimates for design floods. While it is possible to model the snowmelt process with or without rainfall, such models are complex and very data and labour intensive. Thus, their use is usually only warranted for estimating probable maximum floods - the design floods that very important structures, such as large dams, must be designed to withstand.
When adequate flow data are available, there are standard statistical methods for estimating design flows (Chow et al., 1988). However, data are usually not available for the specific site one is interested in. Therefore, the design flow has to be estimated on the basis of recorded flow data from nearby gauging stations. The standard approach involves estimating the flood flow with the required return period (in this case Q100) at each of the gauged sites, using a standard statistical distribution; expressing these in terms of flow per unit area; and interpolating to find the design flow at the site of interest. Often the flow is expressed as Q=KAx where K is a "constant", A is the drainage area and x is another constant. In practice, x is fixed in the range from 0.6 to 1.0, and K values are derived for each gauging site, which the designer then interpolates to obtain K for the specific site. For example, in the Community Watershed Guidebook (Government of British Columbia, 1996), the value of x is given as 0.68 and contours of K are given on a map of the province. Design flows for any particular site can be estimated by interpolating for K (which varies from 7.0 to 0.1) and then computing Q100 as KA0.68. In another initiative, the BC Ministry of Environment, Lands and Parks (MOELP) is currently producing larger scale maps showing values of Q100/A0.78 to become available in 1998 (Obedkoff, Personal Communication).
The above regional approaches provide excellent "first cut" estimates of Q100, but because of the wide spacing of the Water Survey gauges from which the basic flow data were obtained, it is difficult to interpolate accurately between the contours on the map. In an attempt to provide more flexibility, an alternative statistical approach was developed by Russell (1982, 1992) to allow regional flood data to be combined with any available local site flow data for estimating flood flows at the given location.
The method involves the use of a compound distribution made up of a weighted combination of underlying distributions. Initial estimates of the mean and the coefficient of variation of the unit peak flows are assigned on the basis of subjective or regional information. The coefficient of variation is the standard deviation divided by the mean. With flood peak data, it is surprisingly stable over wide areas, which facilitates interpolation. The model can be specified on the basis of regional information alone, and design flows can be computed from that. Other data can be used to update the weights of the component distributions using Bayes’ theorem, thereby increasing the accuracy of the estimates.
For a given watershed this involves making low, probable and high estimates of the mean annual peak flow and its coefficient of variation. The low value should be the one that the hydrologist is 95% sure that the true value will exceed. The probable is the best estimate. The high value is the one that the hydrologist is 95% sure the true value will not exceed. The hydrologist can make these estimates on the basis of the available data, and on professional judgement and experience. As will be described in the next section, the mean annual flow data has much more regional scatter than the coefficient of variation, suggesting that different estimating approaches may be appropriate. This contrasts with the conventional approach of estimating Q100 at few gauged sites and interpolating between them.
Flow data, gathered by the Water Survey of Canada over the years is now available in CD-ROM format. Data from 1937 flood flows on Vancouver Island were obtained from the HYDAT CD-ROM (version 4.92) and analysed. Floods at stations with 2 years of record or less were discarded as were those for which no drainage area was given, thus reducing the number of stations to 1382, recorded at 70 stations. Of these, 32 stations have a regulated flow regime (R) and 38 have a natural, or uncontrolled flow regime (N). The degree of regulation is not specified, but it usually involves a reservoir of some size in the drainage basin. Since most forest road stream crossings involve "natural" streams without any upstream regulation, the unregulated or "natural" gauging stations are of most interest. However, the regulated stations also provide useful information. In general, one would expect peak flows to be lower and the variability of the flows, as reflected by the standard deviation or coefficient of variation, to be lower in a regulated stream than in a comparable unregulated one. Another distinction was made concerning the geographic location of the stations. The stations located on the west coast of the island (W) were coded differently than the other stations (E). The boundaries between these two regions are based on topographic, climatic and physiographic features and they coincide with the boundaries of the hydrologic homogenous zones featured in the digital map of the MOELP.
Figure 1 shows the relationship between basin size and the unit mean daily peak flow (m3/s km2) for all examined stations on Vancouver Island. The points are coded for regulated or natural flow, and west coast or east coast. In general, the west coast stations have higher unit mean daily flows than the other stations, with smaller basins having higher differences than larger ones. However, stations lying in the central part of the island and stations on the east coast of the island showed little differences. Stations with regulated flow regimes show no visible differences compared to stations with natural flows. The length of record did not seem to influence the mean values significantly, although it is obvious that the estimated mean annual flood value is more reliable with a greater monitoring period.
Although there seems to be a trend of decreasing unit flow with basin area, as one would expect, the trend is quite weak statistically with a r2 of only 0.36. Figure 1 does clearly show that there is considerable variation in unit flows. For example, with a basin size in the range of 100 km2, the highest flow is about 20 times that of the lowest flow. This emphasized the difficulty in developing a practical way of estimating the mean annual flood on an ungauged basin by interpolating from regional flood flow data.
It is clear that more regional flood data is required for the province of BC. Since most culverts in BC have entrance control (meaning that the flow corresponding to any particular water level upstream can be computed), it is relatively simple to measure local peak flow data from existing culverts using a peak flow gauge, such as that described in the Appendix.

Figure 1: AREA VERSUS UNIT DAILY MEAN
Figure 2 shows the number of years of record at each station versus the coefficient of variation of the annual peak flows recorded at that station. The degree of scatter is roughly what one would expect from random samples of varying size from a population with a coefficient of variation of between 0.4 and 0.5. There seems to be no distinct patterns for the gauges on streams with regulated or unregulated flow regimes or in the east or the west regions of Vancouver Island. However, one would expect that the values for the regulated stations are lower than they would have been in the pre-regulated states. The main conclusion that can be drawn from Figure 2 is that there is relatively little variation in the coefficient of variation, which suggests that it should be possible to estimate the coefficient of variation at an ungauged site with a high degree of confidence by interpolating from regional estimates.
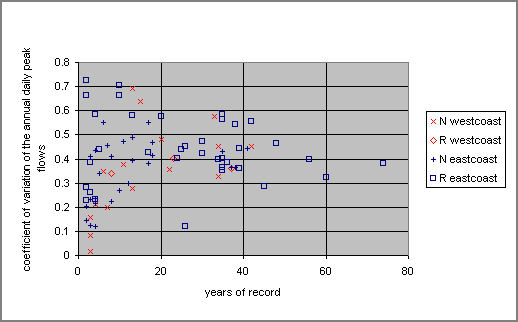
Figure 2: YEARS OF RECORD VERSUS THE COEFFICIENT OF VARIATION
Small culverts and bridges can be sized by measuring the stream cross sectional area and multiplying it by 3.0 (the California method, specified in the BC Forest Practices Code). This is a conservative but simple method that is based on data from the actual site.
When the designer is sure that the larger floods at the site result from rainfall, a rainfall modelling approach may be suitable for estimating Q100. However, it would be wise to compare the result with the actual flow capacity of the stream at normal high water levels and with estimates of Q100 based on regional data.
In other cases, a statistical approach seems most suitable for estimating Q100. However, separate estimates of the mean annual flood and its coefficient of variation should be made. The mean annual flood can be estimated on the basis of the high water level, stream cross section, and estimated roughness of the actual stream channel; and/or estimating the mean annual flood from high water levels upstream from nearby existing culverts. The coefficient of variation can be estimated from regional data. The two can be combined to give estimates of Q100 with the use of a computer program, such as the one described above.
A peak stage water level gauge was developed and tested in the Seymour demonstration Forest Watershed of the GVRD. The basic intent was is to capture the signal of water stage for the highest flow and preserve that signal, until it is reset by the field crew. Requirements for the gauge were that it had to be easy to install, monitor, and reset, and also have inexpensive material costs.
The final design that is now used and is being tested further,
consists of a 1½ inch solid Plexiglas pipe that is mounted on to
a staff at the stream bank. The bottom of the pipe is closed with
fine meshing (fly screen). A tablespoon of Perlite is put into
this pipe. As the water level rises the perlite floats. To keep
the perlite at the highest water level, a strip of Velcro was
applied to a solid ¼ inch Plexiglas rod which is inserted into
the 1½ inch pipe mentioned above. When the water level recedes,
the perlite sticks to the Velcro, leaving a record of the maximum
water level. Measuring at the gauge is simple as it is only
necessary to remove the rod and measure the distance from the
highest perlite mark to the bottom of the rod that corresponds to
the bottom of the pipe where the height is levelled to a
reference point. Resetting the gauge consists of brushing of the
perlite from the Velcro, adding more perlite if needed and
replacing the rod.
Funding provided by Forest Renewal British Columbia is gratefully acknowledged.
British Columbia Government, 1996. Forest Practices Code of British Columbia: Community Watershed Guidebook. Queen’s Printer, Victoria, BC, 117 pp.
Chow, V.T., D.R. Maidment and L.W. Mays, 1988. Applied Hydrology. McGraw-Hill, New York, NY, 572 pp.
Denver Regional Council of Governments, 1969. Urban Storm Drainage, Vols. 1 and 2. Denver, CO.
Heimstra, L.A.V. and B.M. Reich, 1969. Engineering Judgement and Small Area Flood Peaks. Hydrology Papers, No. 19. Colorado State University Press, Denver, CO, 29 pp.
Linsley, R.K., M.A. Kohler, and J.L.H. Paulhus, 1982. Hydrology for Engineers, 3rd Edition. McGraw-Hill, New York. NY, 508 pp.
Loukas, A., M. Quick and S.O. Russell, 1996. A Physically Based Stochastic-Deterministic Procedure for Flood Frequency. Water Resources Management, 10(6), 415pp.
Loukas, A. and M. Quick, 1995. A 24-hour Design Storm for Coastal British Columbia. J. Hydraulic Eng., ASCE, 121(12), 889-899.
Maidment, D.R., 1992. Handbook of Hydrology. McGraw-Hill, New York, NY.
Obedkoff, B., 1997. Ministry of the Environment, Lands and Parks. Personal Communication.
Russell, S.O., 1982. Flood Probability Estimation. J. Hydraulic Eng., ASCE, 108(1), 63-73.
Russell, S.O., 1992. Estimating Flows From Limited Data. Can. J. Civ. Eng., 19 (1), 51-58.
Tolland, L., J.G. Cathcart and S.O. Denis Russell, 1998. Estimating the Q100 in British Columbia: A practical problem in forest hydrology. J. of the American Water Resources Association (in press).
Watts, S.B. (Editor), 1983. Forestry Handbook for British Columbia. 4th ed., University of British Columbia, Vancouver, BC, 611 pp.